벤 다이어그램
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
벤 다이어그램은 1880년 존 벤이 처음 소개한 다이어그램으로, 여러 개의 겹쳐진 닫힌 곡선(주로 원)을 사용하여 집합 간의 관계를 시각적으로 표현한다. 각 원은 하나의 집합을 나타내며, 원의 내부와 외부 영역은 집합의 원소 포함 여부를 의미한다. 벤 다이어그램은 교집합, 합집합, 차집합, 여집합, 대칭차 등의 집합 연산을 표현하며, 논리 연산과 부울 대수 표현에도 활용된다. 20세기에는 벤 다이어그램이 더욱 발전하여 여러 개의 집합을 표현하는 다양한 형태가 개발되었으며, 교육, 밈, 정치적 분석 등 다양한 분야에서 활용된다.
더 읽어볼만한 페이지
- 통계 차트와 다이어그램 - 레이더 차트
레이더 차트는 여러 변수의 상대적 크기를 시각적으로 비교하는 차트로, 중심점에서 방사형으로 뻗어나가는 축을 사용하여 데이터 패턴 파악, 유사성 비교, 이상치 탐색 등에 활용되지만, 면적 왜곡 등의 단점도 존재하여 데이터 해석 시 주의가 필요하다. - 통계 차트와 다이어그램 - 연표
연표는 시간 순서에 따라 사건, 현상, 변화 등을 시각적으로 표현하는 방식으로, 역사 기록에서 시작하여 표 형태로 발전했으며 다양한 분야에서 활용되고 여러 형태로 정보를 제시한다. - 집합론의 기본 개념 - 치역
치역은 함수에서 정의역의 모든 원소에 대한 함숫값들의 집합으로, 공역의 부분집합이며, 함수의 상을 의미하거나 공역 전체를 의미하기도 한다. - 집합론의 기본 개념 - 항등 함수
항등 함수는 집합 X의 각 원소를 자기 자신에게 대응시키는 함수로서, 정의역과 공역이 같은 집합 X에서 단사 함수이자 전사 함수이며, 함수 합성에서 항등원의 역할을 수행하는 중요한 개념이다. - 다이어그램 - 회로도
회로도는 전기 또는 전자 회로의 구성 요소와 연결을 기호와 선으로 나타낸 도식적 표현으로, 표준화된 기호와 규칙을 따르며 전자 제품 설계 및 교육에 필수적인 도구이지만 표기법 통일은 아직 완벽하지 않다. - 다이어그램 - 헤르츠스프룽-러셀 도표
헤르츠스프룽-러셀 도표(HR도표)는 항성의 광도와 표면 온도 관계를 나타내는 그래프로, 항성의 분류, 진화 단계, 물리적 특성을 이해하는 데 필수적인 도구이며, 주계열성, 거성, 초거성 등 다양한 항성의 종류와 분포를 보여주며 항성물리학 발전에 기여한다.
2. 역사
벤 다이어그램은 닫힌 곡선(주로 원)을 사용하여 집합을 표현하고, 이 곡선들의 겹침을 통해 집합 간의 관계를 나타내는 그림이다. 각 곡선 내부의 점은 해당 집합의 원소를 나타내며, 곡선 외부의 점은 해당 집합에 속하지 않는 원소를 나타낸다.
벤 다이어그램은 1880년 존 벤이 철학 잡지 및 과학 저널에 게재한 "명제와 추론의 도해적 및 기계적 표현에 관하여"라는 논문에서 처음 소개되었다. 프랭크 루스키와 마크 웨스턴에 따르면, 형식 논리에서 이러한 유형의 다이어그램 사용은 벤 이전에도 있었지만, 벤이 "그 사용법을 포괄적으로 조사하고 공식화했으며, 그 사용법을 일반화한 최초의 인물"이기 때문에 그와 적절하게 연관되어 있다.
겹치는 원으로 합집합과 교집합을 나타내는 다이어그램은 13세기에 라몬 룰이 처음 소개했으며, 그는 이를 기본 원리의 조합을 설명하는 데 사용했다. 17세기에는 고트프리트 빌헬름 라이프니츠가 유사한 다이어그램을 제작했고(그러나 이 작업의 대부분은 출판되지 않음), 1712년에는 요한 크리스티안 랑에가 크리스티안 바이제가 논리에 기여한 내용을 설명하는 논문에서 유사한 다이어그램을 사용했다. 오일러 다이어그램은 벤 다이어그램과 유사하지만 모든 가능한 합집합과 교집합을 포함하지는 않으며, 18세기에 레온하르트 오일러에 의해 널리 사용되었다.
벤은 "벤 다이어그램"이라는 용어를 사용하지 않았고, 이 개념을 "오일러 원"이라고 불렀다. 그는 1862년에 오일러 다이어그램을 알게 되었고, 오일러 다이어그램을 불 대수에 적용하려 시도하는 동안 "훨씬 나중에" 벤 다이어그램이 떠올랐다고 썼다.[1] 벤은 1880년 논문의 첫 문장에서 오일러 다이어그램이 "일반적인 승인을 얻은" 유일한 논리의 도해적 표현이라고 언급했다.
벤은 자신의 다이어그램을 실험을 통한 물리적 개념의 검증과 유사한 교육적 도구로 보았다. 그는 3개의 집합 다이어그램이 삼단 논법 '모든 ''A''는 어떤 ''B''이다. 어떤 ''B''도 ''C''가 아니다. 따라서 어떤 ''A''도 ''C''가 아니다'를 보여줄 수 있다고 언급했다.[1]
찰스 루트위지 도지슨(루이스 캐럴)은 그의 저서 ''기호 논리''(1896년 출판된 제4판)의 "교사를 위한 부록"에 "벤의 다이어그램 방법"과 "오일러의 다이어그램 방법"을 포함시켰다. "벤 다이어그램"이라는 용어는 이후 1918년 클래런스 어빙 루이스가 그의 저서 ''기호 논리 개요''에서 사용했다.
20세기에는 벤 다이어그램이 더욱 발전했다. 1963년 데이비드 윌슨 헨더슨은 ''n''-겹 회전 대칭을 갖는 ''n''-벤 다이어그램의 존재는 ''n''이 소수임을 의미한다는 것을 보여주었다. 그는 또한 이러한 대칭 벤 다이어그램이 ''n''이 5 또는 7일 때 존재한다는 것을 보여주었다. 2002년, 피터 햄버거는 ''n'' = 11에 대한 대칭 벤 다이어그램을 찾았고, 2003년 그리그스, 킬리언, 새비지는 다른 모든 소수에 대해 대칭 벤 다이어그램이 존재한다는 것을 보여주었다. 이러한 결합된 결과는 회전 대칭 벤 다이어그램이 존재하려면 ''n''이 소수일 필요충분조건임을 보여준다.
벤 다이어그램과 오일러 다이어그램은 1960년대 새로운 수학 운동의 일환으로 집합론 교육에 포함되었다. 그 이후로, 그것들은 읽기와 같은 다른 분야의 커리큘럼에도 채택되었다.
3. 기본 개념 및 표현
''B'': 날 수 있는 생물의 집합
오른쪽 그림을 예로 들면, 주황색 원(집합 ''A'')은 다리가 두 개인 모든 생물을, 푸른 원(집합 ''B'')은 날 수 있는 모든 생물을 나타낸다. 비둘기처럼 두 다리를 가지면서 날 수 있는 생물은 두 원이 겹치는 부분에 위치한다. 인간과 펭귄은 다리가 두 개여서 주황색 원에 있지만, 날지는 못하므로 푸른 원과 겹치지 않는 곳에 있다. 날 수 있지만 다리가 여섯 개인 모기는 푸른 원 중 주황색 원과 겹치지 않는 부분에, 고래나 거미처럼 두 다리를 갖지도 않고 날지도 못하는 생물은 두 원의 바깥에 위치한다.
''A''와 ''B''를 합친 영역은 합집합이며, 두 다리를 가졌거나, 날 수 있거나, 혹은 양쪽 모두에 해당하는 생물들을 모은 것이다. ''A''와 ''B''가 겹쳐진 영역은 교집합이며, 두 다리와 날 수 있는 능력을 모두 갖춘 생물들을 모은 것이다.
벤 다이어그램은 여러 개의 겹쳐진 원으로 구성되며, 각 원은 하나의 집합을 나타낸다. 벤 다이어그램에서 곡선은 가능한 모든 방식으로 겹쳐져 집합 간의 모든 가능한 관계를 보여준다.
3. 1. 집합 연산 표현
집합 연산에 대한 내용은 해당 문서를 참고하라.
3. 2. 논리 연산 표현
벤 다이어그램은 논리 연산을 시각적으로 표현하는 데에도 사용될 수 있다. 벤 다이어그램은 본래 집합 간의 관계를 나타내는 것이지만, 집합 대수와 논리 연산이 부울 대수로서 동일하기 때문에, 논리 연산을 시각적으로 알기 쉽게 표현하는 방법으로 벤 다이어그램이 자주 사용된다.
논리 연산을 벤 다이어그램으로 나타내는 경우, 원은 논리 연산의 입력값을 나타내는 논리 변수에 대응하며, 원의 내부는 해당 변수의 값(진리값)이 참(1 또는 T)임을, 원의 외부는 거짓(0 또는 F)임을 나타낸다. 논리 연산의 출력값을 참으로 만드는 입력값의 조합에 해당하는 영역에 사선을 긋거나 색을 칠함으로써, 입력값과 출력값의 관계를 나타낸다. 예를 들어 논리곱 (AND) P ∧ Q를 벤 다이어그램으로 나타내면 아래 그림과 같다. 이는 집합 ''A''와 집합 ''B''의 교집합 ''A'' ∩ ''B''를 나타내는 벤 다이어그램과 외형은 같지만, 논리 연산 P ∧ Q를 나타내는 것으로 간주할 때, 원은 집합을 의미하는 것이 아니라는 점에 주의해야 한다.
아래 그림은 집합 연산을 나타내는 경우의 벤 다이어그램 표현 방식에 대응하는 표기이며, 검은색 영역은 "해당 입력값의 조합이 발생하지 않음"을 나타낸다.
- 왼쪽 원: P
- 오른쪽 원: Q
4. 확장
벤 다이어그램은 보통 2개나 3개의 집합을 나타내지만, 4개 이상의 집합을 표현하는 것도 가능하다. 4개의 집합을 나타낼 때는 타원을 사용하거나, 구의 표면을 분할하는 방식을 사용할 수 있다.
5개 이상의 집합을 나타내는 벤 다이어그램은 더욱 복잡한 형태를 가지게 되며, 이 과정에서 다이어그램의 대칭성 일부를 잃게 된다. 존 벤은 타원을 사용하여 4개의 집합을 표현하는 벤 다이어그램을 고안했다.
존 벤은 또한 3개의 원으로 시작하여 집합을 추가할 때마다 이전 곡선들과 교차하는 곡선을 추가하는 방식으로, 집합 개수에 제한 없이 벤 다이어그램을 구성하는 방법을 제시했다.
4. 1. 에드워즈-벤 다이어그램
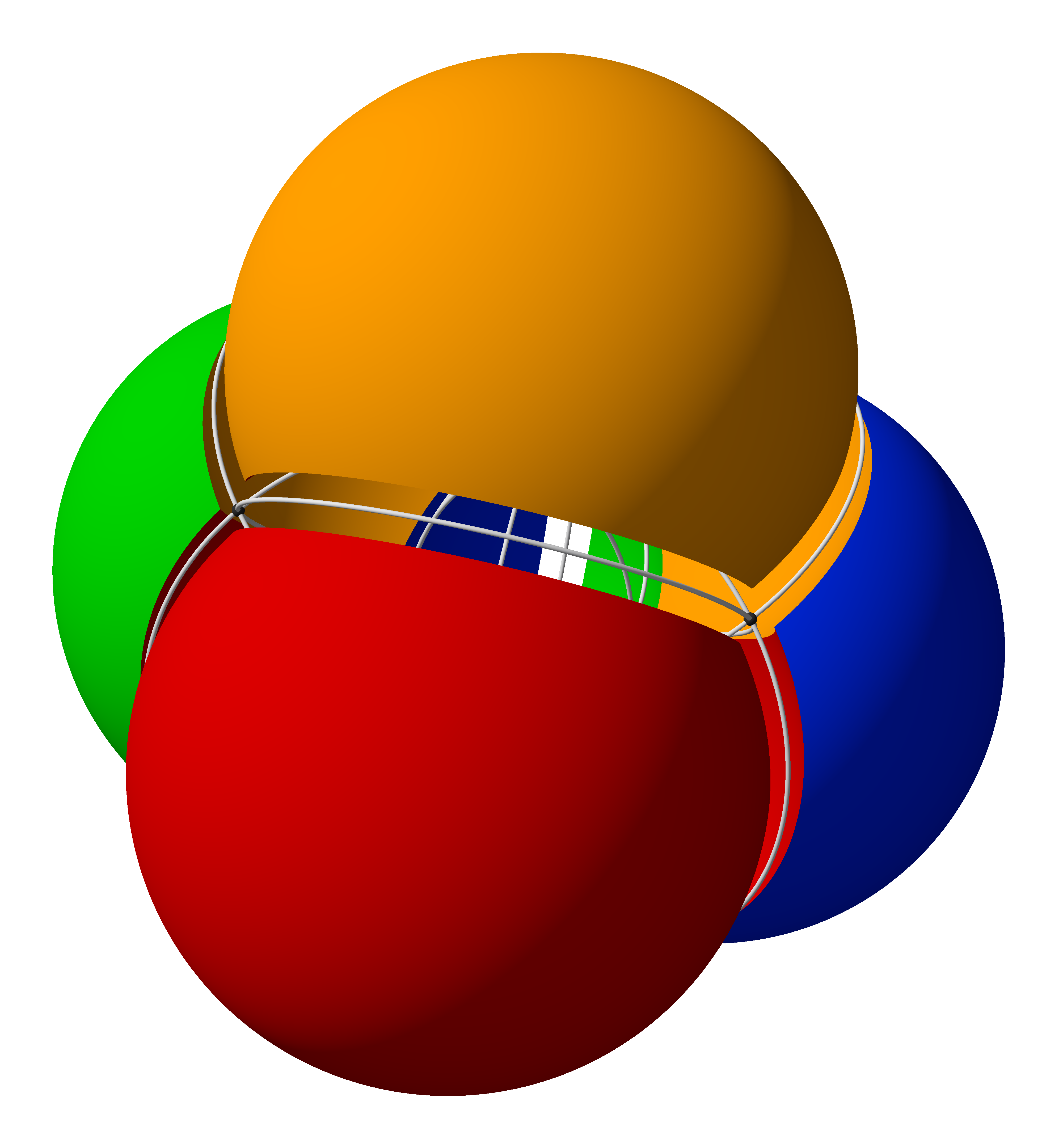
앤서니 윌리엄 페어뱅크 에드워즈는 구 표면을 분할하여 더 많은 집합을 표현할 수 있는 벤 다이어그램을 고안했으며, 이를 에드워즈-벤 다이어그램이라고 한다. 예를 들어, 세 개의 집합은 구의 세 반구를 직각(x = 0, y = 0, z = 0)으로 표현할 수 있다. 네 번째 집합은 테니스 공의 솔기와 같이 적도를 따라 위아래로 감기는 곡선을 추가하여 나타낼 수 있다. 이렇게 만들어진 집합을 평면에 투영하면 톱니 수가 늘어나는 톱니바퀴 모양의 다이어그램이 된다. 이 다이어그램은 벤을 기리는 스테인드글라스 창을 디자인할 때 고안되었다.


5. 관련 개념
오일러 다이어그램은 벤 다이어그램과 유사하지만, 모든 가능한 관계를 반드시 포함하지는 않으며 주어진 문맥에서 실제로 가능한 영역만 포함한다. 벤 다이어그램에서 음영 처리된 영역은 빈 영역을 나타낼 수 있지만, 오일러 다이어그램에서는 해당 영역이 다이어그램에서 누락된다.
존스턴 다이어그램은 벤 다이어그램을 진리표 형태로 나타낸 것이다.
R-다이어그램은 존 F. 랜돌프가 고안한 집합 표현 방법이다.
6. 활용 및 의의
벤 다이어그램은 집합, 확률, 논리, 통계 등 다양한 분야의 개념을 시각적으로 명확하게 표현하고 이해하는 데 도움을 준다.[2] 문제 해결 과정에서 정보를 구조화하고 분석하는 도구로 활용될 수 있다. 교육 현장에서는 집합론, 논리 연산 등을 가르치는 데 유용하게 사용된다.
논리 연산을 벤 다이어그램으로 나타낼 수 있다. 벤 다이어그램은 본래 집합 간의 관계를 나타내는 것이며, 논리 연산에 벤 다이어그램을 사용하는 것은 본래의 사용법은 아니지만, 현실적으로는 집합 대수와 논리 연산이 부울 대수로서 동일하기 때문에, 논리 연산을 시각적으로 알기 쉽게 표현하는 방법으로 벤 다이어그램이 자주 사용된다.
논리 연산을 벤 다이어그램으로 나타내는 경우, 원은 논리 연산의 입력값을 나타내는 논리 변수에 대응하며, 원의 내부는 해당 변수의 값(진리값)이 참(1 또는 T)임을, 원의 외부가 거짓(0 또는 F)임을 나타낸다. 논리 연산의 출력값을 참으로 만드는 입력값의 조합에 해당하는 영역에 사선을 긋거나 색을 칠함으로써, 입력값과 출력값의 관계를 나타낸다. 예를 들어, 그림 4는 왼쪽 원을 P, 오른쪽 원을 Q로 하여, P와 Q의 논리곱 (AND) P ∧ Q를 벤 다이어그램으로 나타낸 것이다. 이는 집합 ''A''와 집합 ''B''의 교집합 ''A'' ∩ ''B''를 나타내는 벤 다이어그램과 외형은 같지만, 논리 연산 P ∧ Q를 나타내는 것으로 간주할 때, 원은 집합을 의미하는 것이 아니라는 점에 주의해야 한다.
아래 그림은 집합 연산을 나타내는 경우의 벤 다이어그램 표현 방식에 대응하는 표기이며, 검은색 영역은 "해당 입력값의 조합이 발생하지 않음"을 나타낸다.
대중문화에서도 벤 다이어그램은 밈 등에서 활용되며, 복잡한 관계를 간결하게 표현하는 데 사용된다.[2]
참조
[1]
간행물
The Venn Behind the Diagram
Institute of Mathematics and its Applications
2023-04
[2]
뉴스
Jesus, Karaoke, And Serial Killers: The Funniest Venn Diagrams The Web Has To Offer
https://www.huffpost[...]
2024-10-02
[3]
뉴스
Scott Walker Gets Mercilessly Mocked By Twitter Users Over Venn Diagram Fail
https://www.huffpost[...]
2024-10-02
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com